Question

MAPS On a map, Wilmington Street, Beech Drive, and Ash Grove Lane appear to all be parallel. The on

ilmington to Ash Grove along Kendall is 820 feet and along Magnolia, 660 feet. If the distance between Beech and

ove along Magnolia is 280 feet, what is the distance between the two streets along Kendall?

Answer 1

The distance between the two streets along Kendall is 347.9 feet.

Solution:

The image of the problem is attached below.

Distance between Wilmington to Ash Grove along Kendall = 820 feet

Distance between Wilmington to Ash Grove along Magnolia = 660 feet

Distance between Beech and Ash Grove along Magnolia = 280 feet

Distance between Wilmington to Beech along Magnolia

= 660 feet – 280 feet

= 380 feet

Let us x be the distance between Wilmington to Beech along Kendall and

820 – x be the distance between Beech and Ash Grove along Kendall.

The given streets are parallel.

By proportionality theorem, parallel lines cut by a transversal are in proportion.

`$\Rightarrow(380)/(280) =(x)/(820-x)`

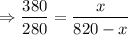
Do cross multiplication.

`$\Rightarrow{380}({820-x}) =280x`

`$\Rightarrow 311600-380x =280x`

`$\Rightarrow 311600 =280x+380x`

`$\Rightarrow 311600 =660x`

`$\Rightarrow x=472.1`

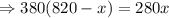
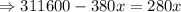
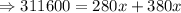
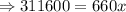
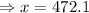
Distance between Beech and Ash Grove along Kendall

= 820 – x

= 820 – 472.1

= 347.9

Hence the distance between the two streets along Kendall is 347.9 feet.