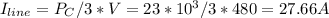Answer:
(a) attached below
(b)
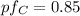
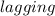
(c)
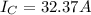
(d)
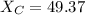 Ω
Ω
(e)
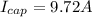 and
and
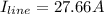
Step-by-step explanation:
Given data:
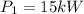
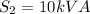
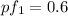
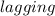
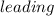
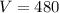
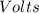
(a) Draw the power triangle for each load and for the combined load.
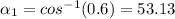 °
°
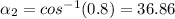 °
°
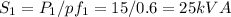
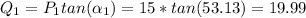 ≅
≅
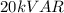
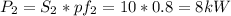
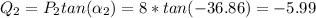 ≅
≅
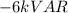
The negative sign means that the load 2 is providing reactive power rather than consuming
Then the combined load will be
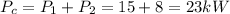

(b) Determine the power factor of the combined load and state whether lagging or leading.
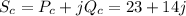
or in the polar form
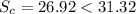 °
°
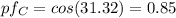
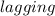
The relationship between Apparent power S and Current I is
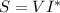
Since there is conjugate of current I therefore, the angle will become negative and hence power factor will be lagging.
(c) Determine the magnitude of the line current from the source.
Current of the combined load can be found by
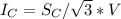
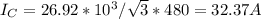
(d) Δ-connected capacitors are now installed in parallel with the combined load. What value of capacitive reactance is needed in each leg of the A to make the source power factor unity?Give your answer in Ω

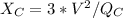
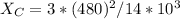 Ω
Ω
(e) Compute the magnitude of the current in each capacitor and the line current from the source.
Current flowing in the capacitor is

Line current flowing from the source is