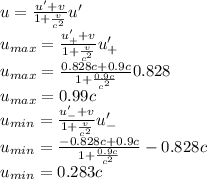Question

A high-speed K0 meson is traveling at β = 0.90 when it decays into a π + and a π − meson. What are the greatest and least speeds that the mesons may have?

Answer 1

greatest speed=0.99c

least speed=0.283c

Step-by-step explanation:

To solve this problem, we have to go to frame of center of mass.

Total available energy fo π + and π - mesons will be difference in their rest energy:

`E_{0,K_(0) }-2E_(0,\pi ) =497Mev-2*139.5Mev\\`

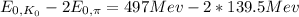
=218 Mev

now we have to assume that both meson have same kinetic energy so each will have K=109 Mev from following equation for kinetic energy we have,

K=(γ-1)
`E_(0,\pi )`

`K=E_(0,\pi)(\frac{1}{\sqrt{1-\beta ^(2) } } -1)\\\frac{1}\sqrt{1-\beta ^(2) }}=(K)/(E_(0,\pi))+1\\ {1-\beta ^(2)=(1)/(((K)/(E_(0,\pi))+1)^2)}\\\beta ^(2)=1-(1)/(((K)/(E_(0,\pi))+1)^2)}\\\beta = +-\sqrt{(1)/(((K)/(E_(0,\pi))+1)^2)}\\\\\\beta =+-\sqrt{1-(1)/(((109Mev)/(139.5Mev+1)^2))`

`u'=+-0.283c`

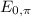
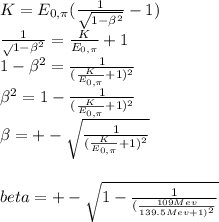
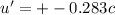
note +-=±

To find speed least and greatest speed of meson we would use relativistic velocity addition equations:

`u=(u'+v)/(1+(v)/(c^(2) ) ) u'\\u_(max) =\frac{u'_(+) +v_{} }{1+(v)/(c^(2) ) } u'_(+) \\u_(max) =(0.828c +0.9c )/(1+(0.9c)/(c^(2) ) ) 0.828\\ u_(max) =0.99c\\u_(min) =\frac{u'_(-) +v_{} }{1+(v)/(c^(2) ) } u'_(-)\\u_(min) =(-0.828c +0.9c )/(1+(0.9c)/(c^(2) ) ) -0.828c\\u_(min) =0.283c`