Question

A porcelain cup of mass 303 g and specific heat 0.260 cal/g-°C contains 161 cm³ of coffee, which has a specific heat of 1.00 cal/g-°C. If the coffee and cup are initially at 71.0 °C, how much ice at 0.00 °C must be added to lower the temperature to 49.0 °C?

Answer 1

`m_i =(1736.702 cal)/(129 cal/gr)=13.46 gr`

So we need to add 13.46 gr of ice in order to reach the final equilibrium temperature of 49 C

Step-by-step explanation:

For this case we need to use the fact that the sum for all the heats involved in the system are 0, since we assume an equilibrium state.

Data given

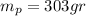`m_p = 303 gr` mass of the porcelain cup

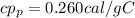`cp_p = 0.260 cal/g C` the specific heat for the porcelain cup

`T_(ip) = T_(ic)= 71 C` initial temperature for the coffee and the porcelain cup.

`V_(c)= 161 cm^3` Volume of the coffee.

We can convert this to m^3 and we got 0.000161m^3 and assuming the density fot the coffee equal to the water 1 Kg/m^3 the mass would be:

`m_c = 1 kg/m^3 *0.000161 m^3 = 0.000161 kg=0.161 Kg`

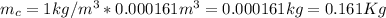
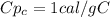`Cp_(c) = 1 cal/g C` Specific heat for the coffee

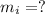`m_i =?` mass of ice required

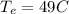`T_e= 49C` equilibrium temperature

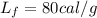`L_f = 80 cal/g` represent the latent heat of fusin since the ice change the state to liquid.

Solution to the problem

Using this formula:

`\sum_(i=1)^n Q_i = 0`

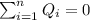
We have this:

`m_p cp_p (T_e -T_(ip)) + m_(c) cp_c (T_e -T_(ic)) +m_i L_f + m_i cp_w (T_e -0) =0`

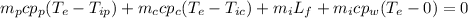
Now we can replace and we have this:

`303 gr *(0.260 cal/g C) (49-71)C + 0.161 gr*(1 cal/g C)(49-71)C +m_i [80 cal/gr+(1cal/g C)(49-0)C]=0`

And now we can solve for
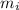`m_i` and we have:

`-1733.16cal -3.542cal +m_i [129 cal/g]=0`

`m_i =(1736.702 cal)/(129 cal/gr)=13.46 gr`

So we need to add 13.46 gr of ice in order to reach the final equilibrium temperature of 49 C