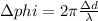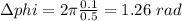Question

You are 2m from one audio speaker and 2.1m from another audio speaker. Both generate the identical sine wave with a frequency of 680 Hz. At your location, what is the phase difference between the waves? Give the answer in radians, using 340m/s as the velocity of sound.

Answer 1

the phase difference is 1.26 radian

Solution:

As per the question:

Distance, d = 2 m

Distance from the other speaker, d' = 2.1 m

Frequency, f = 680 Hz

Speed of sound, v = 340 m/s

Now,

To calculate the phase difference,
`\Delta \phi`:

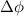Path difference,
`\Delta d = d' - d = 2.1 - 2 = 0.1\ m`

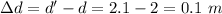
For the wavelength:

`f\lambda = v`

where

c = speed of light in vacuum

`\lambda` = wavelength

Now,

`680* \lambda = 340`

`\lambda = 0.5\ m`

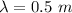
Now,

Phase difference,
`\Delta phi = 2\pi (\Delta d)/(\lambda)`

`\Delta phi = 2\pi (0.1)/(0.5) = 1.26\ rad`