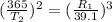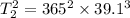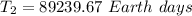Answer:
Step-by-step explanation:
Given
Distance between Pluto and sun is 39.1 times more than the distance between earth and sun
According to Kepler's Law
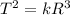
where k=constant
T=time period
R=Radius of orbit
Suppose
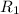 is the radius of orbit of earth and sun
is the radius of orbit of earth and sun
so Distance between Pluto and sun is
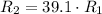
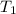 and
and
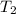 is the time period corresponding to
is the time period corresponding to
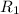 and R_2[/tex]
and R_2[/tex]
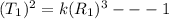
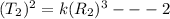
divide 1 and 2