Question

Two identical loudspeakers are driven in phase by the same amplifier. The speakers are positioned a distance of 3.2 m apart. A person stands 4.1 m away from one speaker and 4.8 m away from the other. Calculate the second lowest frequency that results in destructive interference at the point where the person is standing. Assume the speed of sound to be 343 m/s.

Answer 1

f = 735 Hz

Step-by-step explanation:

given,

Person distance from speakers

r₁ = 4.1 m r₂ = 4.8 m

Path difference

d = r₂ - r₁ = 4.8 - 4.1 = 0.7 m

For destructive interference

`d = (n\lambda)/(2)`

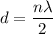
where, n = 1, 3,5..

we know, λ = v/f

`d = (n v)/(2f)`

v is the speed of the sound = 343 m/s

f is the frequency

`f = (n v)/(2d)`

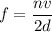
for n = 1

`f = (343)/(2* 0.7)`

f = 245 Hz

for n = 3

`f = (3* 343)/(2* 0.7)`

f = 735 Hz

Hence,the second lowest frequency of the destructive interference is 735 Hz.