Question

The 68-95-99.7 rule tells us how to find the middle 68%, 95% or 99.7% of a normal distribution. suppose we wanted to find numbers a and b so that the middle 80% of a standard normal distribution lies between a and b where a is less than

b. one of the answers below are not true of a and


b. mark the answer that is not true.

Answer 1

The values of a and b are -1.28 and 1.28 respectively.

Explanation:

It is provided that the area of the standard normal distribution between a and b is 80%.

Also it is provided that a < b.

Let us suppose that a = -z and b = z.

Then the probability statement is

`P (a<Z<b)=0.80\\P(-z<Z<z)=0.80`

Simplify the probability statement as follows:

`P(-z<Z<z)=0.80\\P(Z<z)-P(Z<-z)=0.80\\P(Z<z)-[1-P(Z<z)]=0.80\\2P(Z<z)-1=0.80\\P(Z<z) = (1.80)/(2)\\P(Z<z) =0.90`

Use the standard normal distribution table to determine the value of z.

Then the value of z for probability 0.90 is 1.28.

Thus, the value of a and b are:

`a = -z = - 1.28\\b = z = 1.28`

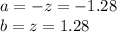
Thus,
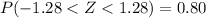`P(-1.28<Z<1.28)=0.80`.