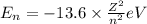Step-by-step explanation:
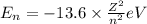
Formula used for the radius of the
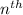 orbit will be,
orbit will be,
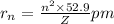 (in pm)
(in pm)
where,
 = energy of
= energy of
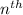 orbit
orbit
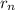 = radius of
= radius of
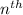 orbit
orbit
n = number of orbit
Z = atomic number
a) The Bohr radius of an electron in the n = 3 orbit of a hydrogen atom.
Z = 1
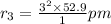
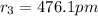
476.1 pm is the Bohr radius of an electron in the n = 3 orbit of a hydrogen atom.
b) The energy (in J) of the atom in part (a)
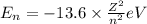


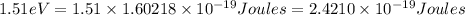
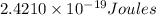 is the energy of n = 3 orbit of a hydrogen atom.
is the energy of n = 3 orbit of a hydrogen atom.
c) The energy of an Li²⁺ ion when its electron is in the n = 3 orbit.
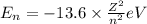
n = 3, Z = 3
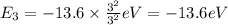
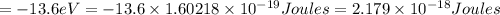
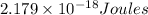 is the energy of an Li²⁺ ion when its electron is in the n = 3 orbit.
is the energy of an Li²⁺ ion when its electron is in the n = 3 orbit.
d) The difference in answers is due to change value of Z in the formula which is am atomic number of the element..