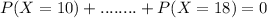Answer:
a)
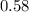
b)
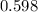
c)
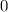
Step-by-step explanation:
Given -
Total sample i.e n
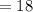
Probability (p)
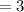 %
%
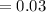
We will use binomial distribution theory for determining the probability of mutated sample
Let X be the number of mutated sample
a) No samples are mutated i.e
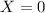
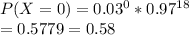
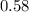
b) At most one sample is mutated
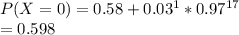
c) More than half the samples are mutated.