Step-by-step explanation:
The sped of sound is given as follows.
C =
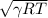
It is known that for hydrogen,
R = 4124 J/kg K
T = 288 k
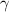 = 1.41
= 1.41
Therefore, calculate the value of
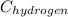 as follows.
as follows.
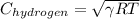
=
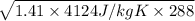
= 1294.1 m/s
For helium,
R = 2077 J/kg K
T = 288 k
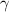 = 1.66
= 1.66
Therefore, calculate the value of
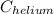 as follows.
as follows.
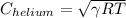
=
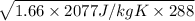
= 996.48 m/s
For nitrogen,
R = 296.8 J/kg K
T = 288 k
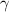 = 1.4
= 1.4
Therefore, calculate the value of
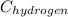 as follows.
as follows.
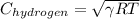
=
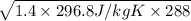
= 345.93 m/s
So, speed of sound in hydrogen is calculated as follows.
=
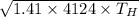
=
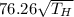
Speed of sound in helium is as follows.
=
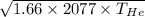
=
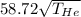
For both the speeds to be equal,
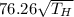 =
=
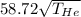
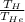 = 0.593
= 0.593
Therefore, we can conclude that the temperature of hydrogen is 0.593 times the temperature of helium.