Question

A square steel bar has a length of 9.8 ftft and a 2.6 inin by 2.6 inin cross section and is subjected to axial tension. The final length is 9.80554 ftnt . The final side length is 2.59952 in in . What is Poisson's ratio for the material? Express your answer to three significant figures.

Answer 1

To solve this problem we will apply the concept related to the Poisson ratio for which the longitudinal strains are related, versus the transversal strains. First we need to calculate the longitudinal strain as follows

`\epsilon_x = (l_f-l_i)/(l_i)`

`\epsilon_x = ((9.80554)-(9.8))/(9.8)`

`\epsilon_x = 0.0005653`

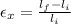
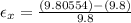
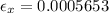
Second we will calculate the lateral strain as follows

`\epsilon_y = (a_f-a_i)/(a_i)`

`\epsilon_y = (2.59952-2.6)/(2.6)`

`\epsilon_y = -0.0001846153`

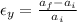
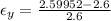
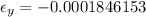
The Poisson's ratio is the relation between the two previous strain, then,

`\upsilon = -(\epsilon_y)/(\epsilon_x)`

`\upsilon = -((-0.0001846153))/(0.0005653)`

`\upsilon = 0.3265`

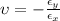
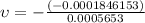
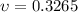
Therefore the Poisson's ratio for the material is 0.3265