hello!

In order to find the vertex of a parabola, we use the following formula:

Please remember that a parabola looks like this:

Now you know what a and b stand for.
In this case, a = -1, and b is 6:

Simplify:
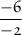

Notes:
- Hope everything is clear.
- Let me know if you have any questions!
- Enjoy your day!
- Always remember: Knowledge is Power :)
Answered by