Answer:
The option x squared ( root index 4 start root x squared end root) is correct
Therefore the equivalent expression to the given expression is
![x^2\sqrt[4]{x^2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/n7rcqgfxszugfcgqv1j0bf9ot3j1vg37ti.png)
Explanation:
Given expression is
![\sqrt[4]{x^(10)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/2q4bgb5xqqv0jeq1rn9yo3lggzbo0szz5e.png)
To find the equivalent expression to the given expression :
![\sqrt[4]{x^(10)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/2q4bgb5xqqv0jeq1rn9yo3lggzbo0szz5e.png)
![=\sqrt[4]{x^(8+2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/7zj3e85xm0ss6dvwpci60w42sr9x7q6tp1.png)
![=\sqrt[4]{x^8.x^2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/3hxsklyuy7xo4hy6t7e4icr7h2wq5r3qjm.png) ( using the property
( using the property
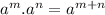 )
)
![=\sqrt[4]{x^(2* 4).x^2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/s49lsq68zuy3nykkry47xtry94hrbl8bzg.png)
![=\sqrt[4]{(x^2)^4x^2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/iznkopteaylicge13oh86uj2zysqb0bi4j.png) ( using the peoperty
( using the peoperty
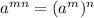 )
)
![=\sqrt[4]{(x^2)^4}* \sqrt[4]{x^2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/omq5l53mt1dux3kzi4e047nbqar524r6qo.png) ( using the property
( using the property
 )
)
![=x^2\sqrt[4]{x^2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/5vfegr06e3sxkiy8vok19y1hqx56qp11tm.png)
Therefore
![\sqrt[4]{x^(10)}=x^2\sqrt[4]{x^2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/zlqvme9ewzyxa1fub42equfu0qqoxrirhn.png)
Therefore the equivalent expression to the given expression is
![x^2\sqrt[4]{x^2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/n7rcqgfxszugfcgqv1j0bf9ot3j1vg37ti.png)
The option "x squared (RootIndex 4 StartRoot x squared EndRoot)" is correct
That is
![x^2\sqrt[4]{x^2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/n7rcqgfxszugfcgqv1j0bf9ot3j1vg37ti.png) is correct
is correct