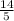Answer:
t =
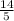
Explanation:
Parallel lines have equal slopes.
calculate the slope m of PQ and then equate the slope of AB to slope of PQ
calculate m using the slope formula
m =
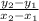
with (x₁, y₁ ) = P (- 2, 4 ) and (x₂, y₂ ) = Q (4, - 1 )
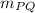 =
=
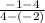 =
=
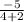 = -
= -

now calculate slope of AB
with (x₁, y₁ ) = A (4, - 3 ) and (x₂, y₂ ) = B (t, - 2 )
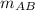 =
=
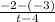 =
=
 =
=
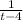
equating the slopes gives
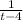 = -
= -
 ( cross- multiply )
( cross- multiply )
5(t - 4) = - 6
5t - 20 = - 6 ( add 20 to both sides )
5t = 14 ( divide both sides by 5 )
t =