Question

Jason and Jeremy work together at a juggling-ball factory. Jason lives 25 miles away from the factory and drives at 60 miles per hour. Jeremy lives 35 miles away from the factory and drives at 70 miles per hour. If they leave their houses at the same time, then

(a) who arrives at the factory first ?
(b) how long is it until the other person arrives?

Answer 1

Jason arrives at the factory first

It takes 5 minutes until the other person arrives

Solution:

The time taken is given by formula:

`Time\ taken = (distance)/(speed)`

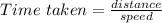
Jason lives 25 miles away from the factory and drives at 60 miles per hour

Therefore, time taken by Jason is:

`Time\ taken = (25)/(60)\ hour`

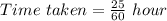
Convert to minutes

1 hour = 60 minutes

Therefore,

`Time\ taken = (25)/(60) * 60\ minutes = 25\ minutes`

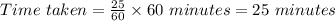
Jeremy lives 35 miles away from the factory and drives at 70 miles per hour

Therefore time taken by Jeremy is:

`Time\ taken = (35)/(70)\ hour\\\\Time\ taken = (35)/(70) * 60\ minutes\\\\Time\ taken = 30\ minutes`

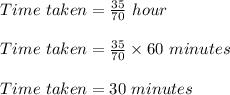
They leave their houses at the same time

25 minutes < 30 minutes

Thus Jason arrives first

Jason arrives to the factory in 25 minutes

Jeremy arrives to the factory in 30 minutes

⇒ 30 - 25 = 5 minutes

Jeremy arrives after Jason by 5 minutes

It takes 5 minutes until the other person arrives