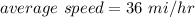Question

Dale travels from city A to city B to city C and back to city A. Each city is exactly 120 miles from the other two. His average rate from city A to city B is 60 mph. His average rate from city B to city C is 40 mph. His average rate from city C to city A is 24 mph. What is Dale's average rate for the entire trip, in miles per hour?

Answer 1

`average\ speed = 36\ mi/hr`

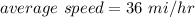
Explanation:

Given:

Each city is exactly 120 miles from the other two.

Average rate from city A to city B = 60 mi/hr

Average rate from city B to city C = 40 mi/hr

Average rate from city c to city A = 24 mi/hr

We need to find the Dale's average rate for the entire trip.

Solution:

First we find the total time and total distance by following way.

Time taken to travel from A to B =
`(Distance)/(Speed) = (120)/(60)= 2\ hr`

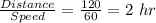
Time taken to travel from B to C =
`(Distance)/(Speed) = (120)/(40)= 3\ hr`

Time taken to travel from C to A =
`(Distance)/(Speed) = (120)/(24)= 5\ hr`

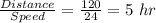
So, total time taken =
`2+3+5=10\ hr`

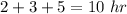
Total distance = 120 + 120 + 120 = 360 miles

Using average speed formula.

`average\ speed = (Total\ distance)/(Total\ time\ taken)`

`average\ speed = (360)/(10)`

`average\ speed = 36\ mi/hr`

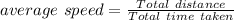
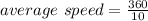
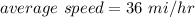
Therefore, the average rate for the entire trip
`average\ speed = 36\ mi/hr`