Question

In addition to continuous radiation, fluorescent lamps emit sharp lines in the visible region from a mercury discharge within the tube. Much of this light has a wavelength of 436 nm. What is the energy (in J) of one photon of this light?

Answer 1

The energy of one photon of light with a wavelength of 436 nm is 4.546 × 10^-19 J.

Step-by-step explanation:

To calculate the energy of one photon, we can use the equation E = hc/λ, where E is the energy, h is Planck's constant (6.626 × 10-34 J·s), c is the speed of light (3.00 × 108 m/s), and λ is the wavelength.

Plugging in the given wavelength of 436 nm (which is equal to 4.36 × 10-7 m) into the equation, we have:

E = (6.626 × 10-34 J·s)(3.00 × 108 m/s) / (4.36 × 10-7 m) = 4.546 × 10-19 J

Therefore, the energy of one photon of light with a wavelength of 436 nm is 4.546 × 10-19 J.

Answer 2

`4.56 x 10^(-19)J`

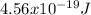
Step-by-step explanation:

Electromagnetic radiations consist of quanta of energy called photons which have energy, E which is equal to:

E = hν.....................................(1)

where h is the Planck's constant which is
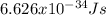`6.626 x10^(-34)Js` and ν is the frequency of light radiation.

But ν = c/λ ....................................(2)

Putting equation (2) into (1), we have

E = hc/λ..........................................(3)

c is the speed of light (c =
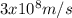`3 x 10^(8)m/s`) while λ is the wavelength of light.

Wavelength λ = 436nm =
`436 x 10^(-9)m`

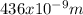
Therefore the energy E of one photon of this light, using equation (3) is

`E=(6.626 x 10^(-34) x3 x10^(8) )/(436 x 10^(-9) ) = 4.56 x 10^(-19) J`