Question

Arrange the following H atom electron transitions in order of increasing frequency of the photon absorbed or emitted:

(a) n = 2 to n = 4
(b) n = 2 to n = 1
(c) n = 2 to n = 5
(d) n = 2 to n = 1

Answer 1

The question is incomplete , complete question is:

Arrange the following H atom electron transitions in order of increasing frequency of the photon absorbed or emitted:

(a) n = 2 to n = 4

(b) n = 2 to n = 1

(c) n = 2 to n = 5

(d) n = 4 to n = 3

Answer:

Hence the order of the transition will be : d < a < c < b

Step-by-step explanation:

`E_n=-13.6* (Z^2)/(n^2)ev`

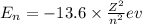
where,

`E_n` = energy of
`n^(th)` orbit

n = number of orbit

Z = atomic number

Energy of n = 1 in an hydrogen atom:

`E_1=-13.6* (1^2)/(1^2)eV=-13.6 eV`

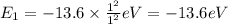
Energy of n = 2 in an hydrogen atom:

`E_2=-13.6* (1^2)/(2^2)eV=-3.40eV`

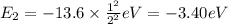
Energy of n = 3 in an hydrogen atom:

`E_3=-13.6* (1^2)/(3^2)eV=-1.51eV`

Energy of n = 4 in an hydrogen atom:

`E_4=-13.6* (1^2)/(4^2)eV=-0.85 eV`

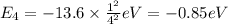
Energy of n = 5 in an hydrogen atom:

`E_5=-13.6* (1^2)/(5^2)eV=-0.544 eV`

a) n = 2 to n = 4 (absorption)

`\Delta E_1= E_4-E_2=-0.85eV-(-3.40eV)=2.55 eV`

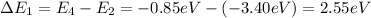
b) n = 2 to n = 1 (emission)

`\Delta E_2= E_1-E_2=-13.6 eV-(-3.40eV)=-10.2 eV`

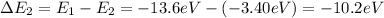
Negative sign indicates that emission will take place.

c) n = 2 to n = 5 (absorption)

`\Delta E_3= E_5-E_2=-0.544 eV-(-3.40eV)=2.856 eV`

d) n = 4 to n = 3 (emission)

`\Delta E_4= E_3-E_4=-1.51 eV-(-0.85 eV)=-0.66 eV`

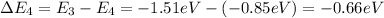
Negative sign indicates that emission will take place.

According to Planck's equation, higher the frequency of the wave higher will be the energy:

`E=h\\u`

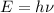
h = Planck's constant

`\\u` frequency of the wave

So, the increasing order of magnitude of the energy difference :

`E_4<E_1<E_3<E_2`

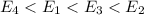
And so will be the increasing order of the frequency of the of the photon absorbed or emitted. Hence the order of the transition will be :

: d < a < c < b