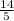Question

let l be the line through A(4,-3) and B(t,-2) that is parallel to the line through P(-2,4) and Q(4,-1) find the value of t

Answer 1

t =
`(14)/(5)`

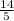
Explanation:

Parallel lines have equal slopes.

calculate the slope m of PQ and then equate the slope of AB to slope of PQ

calculate m using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

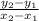
with (x₁, y₁ ) = P (- 2, 4 ) and (x₂, y₂ ) = Q (4, - 1 )

`m_(PQ)` =
`(-1-4)/(4-(-2))` =
`(-5)/(4+2)` = -
`(5)/(6)`

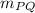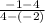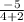now calculate slope of AB

with (x₁, y₁ ) = A (4, - 3 ) and (x₂, y₂ ) = B (t, - 2 )

`m_(AB)` =
`(-2-(-3))/(t-4)` =
`(-2+3)/(t-4)` =
`(1)/(t-4)`

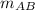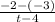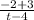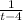
equating the slopes gives

`(1)/(t-4)` = -
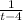`(5)/(6)` ( cross- multiply )

5(t - 4) = - 6

5t - 20 = - 6 ( add 20 to both sides )

5t = 14 ( divide both sides by 5 )

t =
`(14)/(5)`