Question

100 points gor correct answer Identify the base of a triangle in which h=(3x+15) ft and A=(15x+75) ft^2.

b = 30 ft

b = 5x ft

b = 10 ft

Answer 1

b = 10ft

Explanation:

Area = ½ × base × height

15x + 75 = ½ × base × (3x + 15)

30x + 150 = base × (3x + 15)

10(3x + 15) = base × (3x + 15)

base = 10

Answer 2

b = 10

Explanation:

The area (A) of a triangle is calculated as

A =
`(1)/(2)` bh ( b is the base and h the height )

Here h = 3x + 15 and A = 15x + 75, thus

`(1)/(2)` × b × (3x + 15) = 15x + 75

Multiply both sides by 2 to clear the fraction

b(3x + 15) = 30x + 150

Divide both sides by (3x + 15)

b =
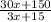`(30x+150)/(3x+15)` ← factor numerator and denominator

=
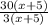`(30(x + 5))/(3(x+5))` ← cancel the factor (x + 5) on numerator/denominator

=
`(30)/(3)`

= 10