1507 are the different ways can 5 baseball players and 4 basketball players be selected from 12 baseball players and 13 basketball players
Solution:
Given that,
5 baseball players and 4 basketball players be selected from 12 baseball players and 13 basketball players
This is a combination problem
Combinations are a way to calculate the total outcomes of an event where order of the outcomes does not matter
The formula is given as:
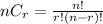
Where n represents the total number of items, and r represents the number of items being chosen at a time
Let us first calculate 5 baseball players from 12 baseball players
Here, n = 12 and r = 5
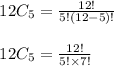
For a number n, the factorial of n can be written as:
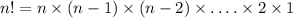
Therefore,
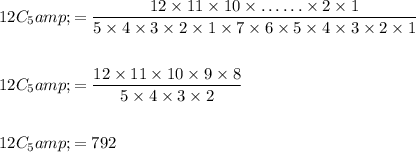
Similarly, 4 basketball players be selected 13 basketball players
n = 13 and r = 4
Similarly we get,
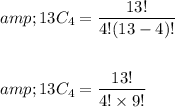
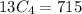
Thus total number of ways are:
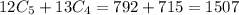
Thus there are 1507 different ways