Question

Solve the following by using mathematical Induction. For >/ 1

1^2+2^2+3^3+......+ n^2 = 1/6 n(n+1)(2n+[)

Answer 1

See explanation

Explanation:

Prove that

`1^2+2^2+3^3+...+n^2=(1)/(6)n(n+1)(2n+1)`

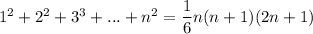
1. When
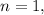`n=1,` we have

• in left part
  `1^2=1;`

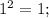
• in right part
  `(1)/(6)\cdot 1\cdot (1+1)\cdot (2\cdot 1+1)=(1)/(6)\cdot 1\cdot 2\cdot 3=1.`

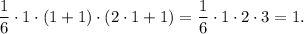
2. Assume that for all
`k` following equality is true

`1^2+2^2+3^3+...+k^2=(1)/(6)k(k+1)(2k+1)`

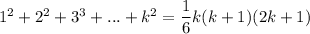
3. Prove that for
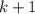`k+1` the following equality is true too.

`1^2+2^2+3^3+...+(k+1)^2=(1)/(6)(k+1)((k+1)+1)(2(k+1)+1)`

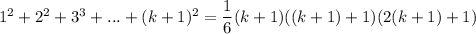
Consider left part:

`1^2+2^2+3^2+...+(k+1)^2=\\ \\=(1^2+2^2+3^3+...+k^2)+(k+1)^2=\\ \\=(1)/(6)k(k+1)(2k+1)+(k+1)^2=\\ \\=(k+1)\left((1)/(6)k(2k+1)+k+1\right)=\\ \\=(k+1)(2k^2+k+6k+6)/(6)=\\ \\=(k+1)(2k^2+7k+6)/(6)=\\ \\=(k+1)(2k^2+4k+3k+6)/(6)=\\ \\=(k+1)(2k(k+2)+3(k+2))/(6)=\\ \\=(k+1)((k+2)(2k+3))/(6)`

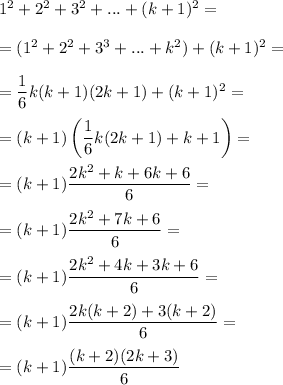
Consider right part:

`(1)/(6)(k+1)((k+1)+1)(2(k+1)+1)=\\ \\(1)/(6)(k+1)(k+2)(2k+3)`

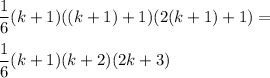
We get the same left and right parts, so the equality is true for
`k+1.`

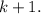
By mathematical induction, this equality is true for all n.