Question

The CEO of a large electric utility company claims that 80 percent of his 1,000,000 customers are very satisfied with the service they receive. To test this claim, the local newspaper surveyed 100 customers, using simple random sampling. After performing the appropriate statistical test, they find the p-value to be 0.894. What conclusion can we make?

Answer 1

Conclusion: The proportion of customers satisfied with the service they receive from the large electric utility company is different from 80%, the claim made by the CEO.

Explanation:

To test the claim made by the CEO of a large electric utility company the newspaper must conduct a hypothesis test for one proportion.

Assumption:

The significance level (α) of the test can be assumed to be 5%.

Hypothesis:

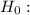`H_(0):` The proportion of customers satisfied with the service they receive is 0.80, i.e.
`p=0.80`

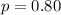
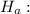`H_(a):` The proportion of customers satisfied with the service they receive is different from 0.80, i.e.
`p\\eq 0.80`

Decision Rule:

If the p-value of the test is less than the significance level (α) then the null hypothesis may be rejected. But if the p-value is more than the significance level (α) then we cannot reject the null hypothesis.

Test Statistics:

As the sample size is large, i.e.n = 100 > 30, then according to the central limit theorem sampling distribution of sample proportion will follow the normal distribution.

The test statistic used is:

`z=\frac{\hat p-p}{\frac{√(p(1-p))} {n} }`

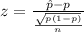
Given:

The p-value of the hypothesis test is computed to be 0.894.

That is:

`p-value=0.894>\alpha =0.05`

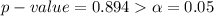
This implies that we fail to reject the null hypothesis at 5% level of significance.

Conclusion:

The null hypothesis was failed to be rejected at 5% level of significance.

Thus, concluding that the proportion of customers satisfied with the service they receive from the large electric utility company is different from 80%, the claim made by the CEO.