Question

As we learned in class if a material’s crystal structure is known a theoretical density, ????, can be computed from a tiny fundamental unit using the formula ???? = ???????? ????c???????? Iron has a BCC crystal structure, an atomic radius of 0.124 nm, and an atomic weight of 55.85 g/mol. Compute and compare its theoretical density with its experimentally measured density of 7.87 g/cm^3.

Answer 1

Answer : Yes, theoretical density can be computed from a tiny fundamental unit using the formula
`\rho=(Z* M)/(N_(A)* a^(3))`.

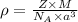Explanation :

Nearest neighbor distance, r =
`0.124nm=1.24* 10^(-8)cm`
`(1nm=10^(-7)cm)`

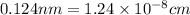
Atomic mass (M) = 55.85 g/mol

Avogadro's number
`(N_(A))=6.022* 10^(23) mol^(-1)`

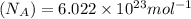
For BCC = Z = 2

Given density =
`7.87g/cm^3`

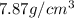
First we have to calculate the cubing of edge length of unit cell for BCC crystal lattice.

For BCC lattice :
`a^3=((4r)/(√(3)))^3=((4* 1.24* 10^(-8)cm)/(√(3)))^3=2.35* 10^(-23)cm^3`

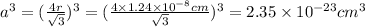
Now we have to calculate the density of unit cell for BCC crystal lattice.

Formula used :

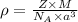`\rho=(Z* M)/(N_(A)* a^(3))` .............(1)

where,

`\rho` = density

Z = number of atom in unit cell (for BCC = 2)

M = atomic mass

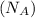`(N_(A))` = Avogadro's number

a = edge length of unit cell

Now put all the values in above formula (1), we get

`\rho=(2* (55.85g/mol))/((6.022* 10^(23)mol^(-1)) * (2.35* 10^(-23)Cm^3))=7.89g/Cm^(3)`

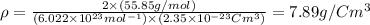
From this information we conclude that, the given density is approximately equal to the given density.

Yes, theoretical density can be computed from a tiny fundamental unit using the formula
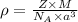`\rho=(Z* M)/(N_(A)* a^(3))`.