Question

A differential equation is given. Classify it as an ordinary differential equation​ (ODE) or a partial differential equation​ (PDE), give the​ order, and indicate the independent and dependent variables. If the equation is an ordinary differential​ equation, indicate whether the equation is linear or nonlinear.

5 (d^2x/dt^2) + 4 (dx/dt) + 9x = 2 Cos 3t

Answer 1

the equation
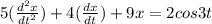`5((d^(2)x )/(dt^(2) )) +4((dx)/(dt))+9x=2cos3t` is a partial differential equation(PDE) because it contains unknown multi variables and their derivatives. This is a PDE of order 2.

The independent variable is x while the dependent variable is t.

The PDE is Linear.

Explanation:

Partial Differential Equation (PDE): This is a differential equation that contains multi variables and their derivatives.

Ordinary Differential Equation (ODE): this is a differential equation containing a function of one independent variable and its derivatives.