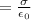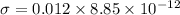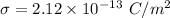Question

The electric flux through a square-shaped area of side 5 cm near a very large, thin, uniformly-charged sheet is found to be 3\times 10^{-5}~\text{N}\cdot\text{m}^2/\text{C}3×10 ​−5 ​​ N⋅m ​2 ​​ /C when the area is parallel to the sheet of charge. Find the charge density on the sheet.

Answer 1

Step-by-step explanation:

Given

side of square shape
`a=5\ cm`

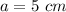
Electric flux
`\phi =3* 10^(-5)\ N.m^2/C`

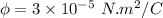
Permittivity of free space
`\epsilon_0=8.85* 10^(-12) (C^2)/(N.m^2)`

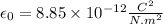
Flux is given by

`\phi =EA\cos \theta`

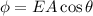
where E=electric field strength

A=area

`\theta`=Angle between Electric field and area vector

`E=(\phi )/(A\cos (0))`

`E=(3* 10^(-5))/(25* 10^(-4)* \cos(0))`

`E=0.012\ N/C`

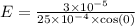
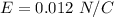
and Electric field by a uniformly charged sheet is given by

`E=(\sigma )/(2\epsilon_0)`

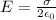
where
`\sigma`=charge density

`=(\sigma )/(\epsilon_0)`

`\sigma =0.012* 8.85* 10^(-12)`

`\sigma =2.12* 10^(-13)\ C/m^2`