Answer:
Part a: The equation is
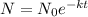
Part b: The half life of the material is 2.4 days.
Explanation:
Part a
The relation is given as
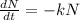
Rearranging the equation gives
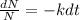
Integrating and simplifying the equation as
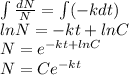
This is the equation of radioactive decay of the radioactive material. For estimation of C consider following IVP where t=0,N=N_o so the equation becomes
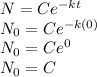
Now substituting the value of C in the equation gives
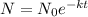
This is the relation of concentration of unstable radioactive material at a given time .
Part b
From the given data the equation becomes as

Now half like is defined as the time when the quantity is exact half, i.e. N/N_o =0.5 so
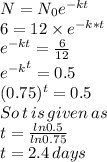
So the half life of the material is 2.4 days.