Question

2. Lab groups of three are to be randomly formed (without replacement) from a class that contains five engineers and four non-engineers. (8pts) (a) How many different lab groups are possible

Answer 1

The number of different lab groups possible is 84.

Explanation:

Given:

A class consists of 5 engineers and 4 non-engineers.

A lab groups of 3 are to be formed of these 9 students.

The problem can be solved using combinations.

Combinations is the number of ways to select k items from a group of n items without replacement. The order of the arrangement does not matter in combinations.

The combination of k items from n items is:
`{n\choose k}=(n!)/(k!(n-k)!)`

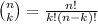
Compute the number of different lab groups possible as follows:

The number of ways of selecting 3 students from 9 is =
`{n\choose k}={9\choose 3}`

`=(9!)/(3!(9 - 3)!)\\=(9!)/(3!* 6!)\\=(362880)/(6*720)\\ =84`

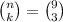
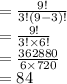
Thus, the number of different lab groups possible is 84.