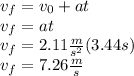Answer:
a.
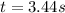
b.
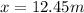
c.
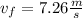
Step-by-step explanation:
The bicyclist's friend moves with constant speed. So, we have:

Th bicyclist moves with constant acceleration and starts at rest (
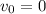 ). So, we have:
). So, we have:
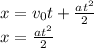
a. When he catches his friend, both travels the same distance, thus:
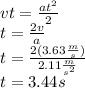
b. We can use any of the distance equations, since both travels the same distance:
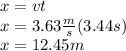
c. The bicyclist final speed is: