Answer : The energy removed must be, -34.67 kJ
Solution :
The process involved in this problem are :
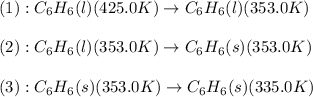
The expression used will be:
![\Delta H=[m* c_(p,l)* (T_(final)-T_(initial))]+m* \Delta H_(fusion)+[m* c_(p,s)* (T_(final)-T_(initial))]](https://img.qammunity.org/2021/formulas/chemistry/high-school/vtpgimsky2sg2h69dvpozjimfbo9tdfqr9.png)
where,
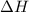 = heat available for the reaction =
= heat available for the reaction =
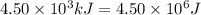
m = mass of benzene = 125 g
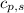 = specific heat of solid benzene =
= specific heat of solid benzene =
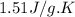
 = specific heat of liquid benzene =
= specific heat of liquid benzene =
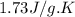
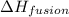 = enthalpy change for fusion =
= enthalpy change for fusion =
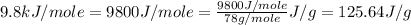
Molar mass of benzene = 78 g/mole
Now put all the given values in the above expression, we get:
![\Delta H=[125g* 1.73J/g.K* (353-425)K]+125g* -125.64J/g+[125g* 1.51J/g.K* (335-353)K]](https://img.qammunity.org/2021/formulas/chemistry/high-school/6i719rhpiyvictdmz43kcu60eo1qopn3ux.png)

Therefore, the energy removed must be, -34.67 kJ