Answer:
Part a:
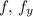 is continuous at the initial value (0,0) so due to Picardi theorem there exists an interval such that the IVP has a unique solution.
is continuous at the initial value (0,0) so due to Picardi theorem there exists an interval such that the IVP has a unique solution.
Part b:
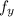 is not continuous at the initial value (0,0) so due to Picardi theorem there does not exist an interval such that the IVP has a unique solution.
is not continuous at the initial value (0,0) so due to Picardi theorem there does not exist an interval such that the IVP has a unique solution.
part c:
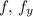 is continuous at the initial value (0,1) so due to Picardi theorem there exists an interval such that the IVP has a unique solution.
is continuous at the initial value (0,1) so due to Picardi theorem there exists an interval such that the IVP has a unique solution.
Explanation:
Part a
as

Let

Now derivative wrt y is given as
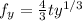
Finding continuity via the initial value
 is continuous on
is continuous on
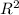 also
also
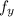 is also continuous on
is also continuous on
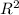
Also
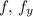 is continuous at the initial value (0,0) so due to Picardi theorem there exists an interval such that the IVP has a unique solution.
is continuous at the initial value (0,0) so due to Picardi theorem there exists an interval such that the IVP has a unique solution.
Part b
as
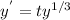
Let
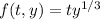
Now derivative wrt y is given as
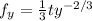
Finding continuity via the initial value
 is continuous on
is continuous on
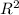 also
also
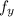 is also continuous on
is also continuous on
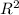
Also
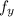 is not continuous at the initial value (0,0) so due to Picardi theorem there does not exist an interval such that the IVP has a unique solution.
is not continuous at the initial value (0,0) so due to Picardi theorem there does not exist an interval such that the IVP has a unique solution.
Part c
as
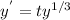
Let
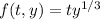
Now derivative wrt y is given as
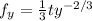
Finding continuity via the initial value
 is continuous on
is continuous on
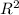 also
also
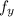 is also continuous on
is also continuous on
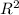 when
when
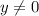
Also
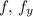 is continuous at the initial value (0,1) so due to Picardi theorem there exists an interval such that the IVP has a unique solution.
is continuous at the initial value (0,1) so due to Picardi theorem there exists an interval such that the IVP has a unique solution.