Question

A jet plane is cruising at 300 m/s when suddenly the pilot turns the engines up to full throttle. After traveling 4.9 km , the jet is moving with a speed of 400 m/s.

a. What is the jet's acceleration, assuming it to be a constant acceleration?
b-Is your answer reasonable ? Explain.

Answer 1

a. 7.14 m/s2

b reasonable

Step-by-step explanation:

We can use the following equation of motion to find out the distance traveled by the jet:

`v^2 - v_0^2 = 2a\Delta s`

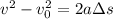
where v = 400 m/s is the final velocity of the jet,
`v_0` = 300m/s is the initial velocity of the jet, a = acceleration of the jet, which we are looking for, and
`\Delta s` = 4.9km = 4900 m is the distance traveled:

`400^2 - 300^2 =  2a4900`

`160000 - 90000 = 9800a`

`9800a = 70000`

`a = 70000 / 9800 = 7.14 m/s^2`

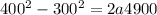
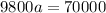
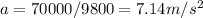
b. This answer is reasonable, as the jet rate increases from 300m/s to 400m/s within 4900 m distance. So it requires a fast rate of 7.14 m/s2

Answer 2

a)
`7.1(m)/(s^(2))`

b) Yes

Step-by-step explanation:

a) For an object with constant acceleration we should use the Galileo kinematic equation:

`v^(2)=v_(0)^(2)+2a\varDelta x` (1)

with v the final velocity vo the initial velocity, a the acceleration and
`\varDelta x` the displacement to change velocity from vo to v at constant acceleration. Solving (1) for a:

`a=(v^(2)-v_(0)^(2))/(2\varDelta x)=(400^(2)-300^(2))/(2(4900))`

`a=7.1(m)/(s^(2))`

That acceleration is lower than acceleration of gravity g= 9.8
`(m)/(s^(2))` and a jet plan is made to support accelerations higher than g and a profesional pilot trained to support it, so 7.1\frac{m}{s^{2}} is a reasonable acceleration for a jet plane.