Question

A ball is thrown horizontally off a cliff. If the initial speed of the ball is (15.0 + A) m/s and the cliff is (25.0 + B) m high, how far from the base of the cliff will the ball land in the water below? Calculate the answer in meters (m) and round to three significant figures.A=4B=54

Answer 1

76.3 m

Step-by-step explanation:

We are given that

Initial speed of the ball,u=(15+A)m/s

Height of cliff,h=(25.9+B) m

We have to find the distance from the base of the cliff the ball will land in the water below.

A=4 and B=54

Distance=
`u\sqrt{(2h)/(g)}`

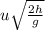
Using the formula and substitute the values

`D=(15+4)\sqrt{(2(25+54))/(9.8)}`

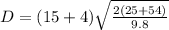
Because
`g=9.8m/s^2`

`D=19\sqrt{(158)/(9.8)}`

D=76.3

Hence, the distance from the base of the cliff the ball will land in the water below=76.3 m