Question

If the angular size of a tree at a distance of 0.5 miles is 1/2, how tall is the tree

Answer 1

The tall of the tree is 23.048 ft.

Solution:

Given data:

Angular size of a tree =
`\left((1)/(2)\right)^(\circ)`

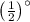
Distance = 0.5 miles = 2640 feet

To find the tall of the tree:

Formula to calculate the height of the tree is

`$\text{Physical size}= \text{Angular size}*\frac{2\pi* \text{distance}}{360^(\circ)}`

`$ = \left((1)/(2)\right)^(\circ)*(2\pi* 2640)/(360^(\circ))`

`$ = \left((1)/(2)\right)^(\circ)*(44\pi)/(3^(\circ))`

`$ = 23.048`

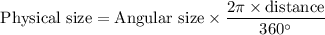
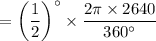
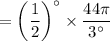
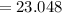
Physical size = 23.048 ft

Hence the tall of the tree is 23.048 ft.