Answer:
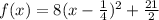
or
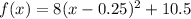
Explanation:
we have
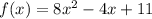
This is a vertical parabola open upward (because the leading coefficient is positive)
The vertex is a minimum
Convert to vertex form
Factor the leading coefficient
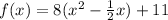
Complete the square. Remember to balance the equation by adding the same constants to each side.
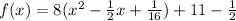
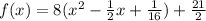
Rewrite as perfect squares
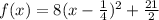 ----> equation in vertex form
----> equation in vertex form
or
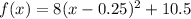
The vertex is the point (0.25,10.5)