What are the coordinates of the x-intercepts of the parabola y = x² - 8x + 15? (3, 0) and (5, 0) (3, 0) and (-5, 0) (-3, 0) and (5, 0) (-3, 0) and (-5, 0)

Question

asked Sep 16, 2021 225k views

1 Answer

Dundar Durma · Answer 1 · 2021-09-22T09:53:28+0000

Answer:

(3, 0) and (5, 0)

Explanation:

we have

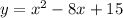
y=x^(2)-8x+15

we know that

The x-intercepts are the values of x when the value of y is equal to zero

so

For y=0

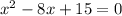
x^(2)-8x+15=0

The formula to solve a quadratic equation of the form

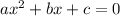
ax^(2) +bx+c=0

is equal to

$x=\frac{-b\pm\sqrt{b^(2)-4ac}} {2a}$

in this problem we have

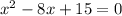
x^(2)-8x+15=0

so

$a=1\\b=-8\\c=15$

substitute in the formula

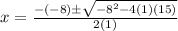
$x=\frac{-(-8)\pm\sqrt{-8^(2)-4(1)(15)}} {2(1)}$

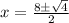
$x=\frac{8\pm√(4)} {2}$

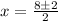
$x=\frac{8\pm2} {2}$

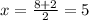
$x=\frac{8+2} {2}=5$

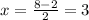
$x=\frac{8-2} {2}=3$

so

x=3, x=5

therefore

The x-intercepts are (3,0) and (5,0)