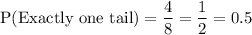Question

Find the probability for the experiment of tossing a coin three times. Use the sample space S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}.

1. The probability of getting exactly one tail
2. The probability of getting exactly two tails
3. The probability of getting a head on the first toss
4. The probability of getting a tail on the last toss
5. The probability of getting at least one head
6. The probability of getting at least two heads

Answer 1

1) 0.375

2) 0.375

3) 0.5

4) 0.5

5) 0.875

6) 0.5

Explanation:

We are given the following in the question:

Sample space, S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}.

`\text{Probability} = \displaystyle\frac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}`

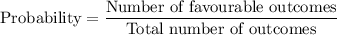
1. The probability of getting exactly one tail

P(Exactly one tail)

Favorable outcomes ={HHT, HTH, THH}

`\text{P(Exactly one tail)} = (3)/(8) = 0.375`

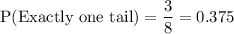
2. The probability of getting exactly two tails

P(Exactly two tail)

Favorable outcomes ={ HTT,THT, TTH}

`\text{P(Exactly two tail)} = (3)/(8) = 0.375`

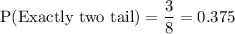
3. The probability of getting a head on the first toss

P(head on the first toss)

Favorable outcomes ={HHH, HHT, HTH, HTT}

`\text{P(head on the first toss)} = (4)/(8) = (1)/(2) = 0.5`

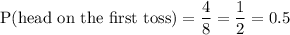
4. The probability of getting a tail on the last toss

P(tail on the last toss)

Favorable outcomes ={HHT,HTT,THT,TTT}

`\text{P(tail on the last toss)} = (4)/(8) = (1)/(2) = 0.5`

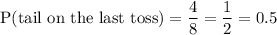
5. The probability of getting at least one head

P(at least one head)

Favorable outcomes ={HHH, HHT, HTH, HTT, THH, THT, TTH}

`\text{P(at least one head)} = (7)/(8) = 0.875`

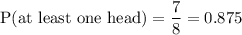
6. The probability of getting at least two heads

P(Exactly one tail)

Favorable outcomes ={HHH, HHT, HTH,THH}

`\text{P(Exactly one tail)} = (4)/(8) = (1)/(2) = 0.5`