Question

How do I solve this? Please show steps clearly so i can understand, thank you

Answer 1

The value of
`x=8`.

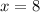Explanation:

Given:

`(x+3)/(x)-(x+1)/(x+4)=(5)/(x)`

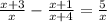
We need to solve this equation.

Solution:

First combining equation having same denominators we get;

`(x+3)/(x)-(5)/(x)=(x+1)/(x+4)`

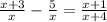
Now denominators are common so we will solve the numerators we get;

`(x+3-5)/(x)=(x+1)/(x+4)\\\\(x-2)/(x)=(x+1)/(x+4)`

Now by cross multiplication we get;

`(x-2)(x+4)=x(x+1)`

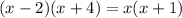
Now Applying distributive property we get;

`x^2+4x-2x-8=x^2+x\\\\x^2+2x-8=x^2+x`

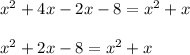
Now Combining the like terms we get;

`x^2+2x-x^2-x=8\\\\x=8`

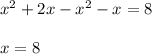
Hence on solving we get the value of
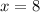`x=8`.