Question

A uniformly charged ring of radius 10.0 cm has a total charge of 78.0 μC. Find the electric field on the axis of the ring at the following distances from the center of the ring. (Choose the x-axis to point along the axis of the ring.)(a) 1.00 cm(b) 5.00 cm(c) 30.0 cm(d) 100 cm

Answer 1

6908316.619 N/C

25087609.3949 N/C

6652357.02259 N/C

690831.6619 N/C

Step-by-step explanation:

x = Distance from the ring

R = Radius of ring = 10 cm

q = Charge = 78 μC

k = Coulomb constant =
`8.99* 10^(9)\ Nm^2/C^2`

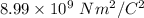
Electric field at a point x is from a ring given by

`E=(kqx)/((x^2+r^2)^(1.5))`

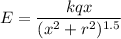
For 1 cm

`E=(kqx)/((x^2+r^2)^(1.5))\\\Rightarrow E=(8.99* 10^9* 78* 10^(-6)* 0.01)/((0.01^2+0.1^2)^(1.5))\\\Rightarrow E=6908316.619\ N/C`

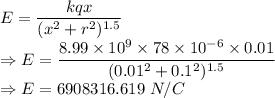
The electric field is 6908316.619 N/C

For 5 cm

`E=(kqx)/((x^2+r^2)^(1.5))\\\Rightarrow E=(8.99* 10^9* 78* 10^(-6)* 0.05)/((0.05^2+0.1^2)^(1.5))\\\Rightarrow E=25087609.3949\ N/C`

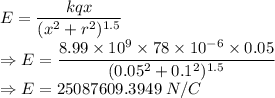
The electric field is 25087609.3949 N/C

For 30 cm

`E=(kqx)/((x^2+r^2)^(1.5))\\\Rightarrow E=(8.99* 10^9* 78* 10^(-6)* 0.3)/((0.3^2+0.1^2)^(1.5))\\\Rightarrow E=6652357.02259\ N/C`

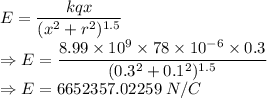
The electric field is 6652357.02259 N/C

For 100 cm

`E=(kqx)/((x^2+r^2)^(1.5))\\\Rightarrow E=(8.99* 10^9* 78* 10^(-6)* 1)/((1^2+0.1^2)^(1.5))\\\Rightarrow E=690831.6619\ N/C`

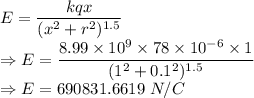
The electric field is 690831.6619 N/C