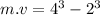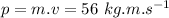Answer:
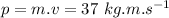
Step-by-step explanation:
Given:
- The initial position of the block,
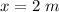
- mass of the block,
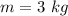
- final position of the block,
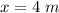
WE know from the Newton's second law:
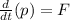
where:
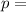 momentum
momentum
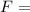 force
force
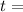 times
times
Now put the values
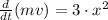
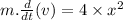
Now integrate both sides from final limit to initial:
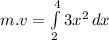
![m.v=[(3x^3)/(3) ]^4_2](https://img.qammunity.org/2021/formulas/physics/college/jrjsdlex4f52caw9t3apvf4wysj4k76r39.png)