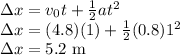Question

A sled starts from rest at the top of a hill and slides down with a constant acceleration. At some later time it is 14.4 m from the top; 2.00 s after that it is 25.6 m from the top, 2.00 slater 40.0 m from the top, and 2.00 s later it is 57.6 m from the top.

(a) What is the magnitude of the average velocity of the sled during each of the 2.00-s intervals after passing the 14.4-m point?
(b) What is the acceleration of the sled?
(c) What is the speed of the sled when it passes the 14.4-m point?
(d) How much time did it take to go from the top to the 14.4-m point?
(e) How far did the sled go during the first second after passing the 14.4-m point?

Answer 1

(a) 5.6 m/s, 7.2 m/s, and 8.8 m/s, respectively.

(b) 0.8 m/s^2

(c) 4.8 m/s

(d) 6 s

(e) 5.2 m

Step-by-step explanation:

(a) The average velocity is equal to the total displacement divided by total time.

For the first 2s. interval:

`V_(\rm avg) = (\Delta x )/(\Delta t) = (25.6 - 14.4)/(2) = 5.6~{\rm m/s}`

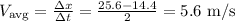
For the second 2s. interval:

`V_(\rm avg) = (40 - 25.6)/(2) = 7.2~{\rm m/s}`

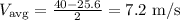
For the third 2s. interval:

`V_(\rm avg) = (57.6 - 40)/(2) = 8.8~{\rm m/s}`

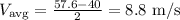
(b) Every 2 s. the velocity increases 1.6 m/s. Therefore, for each second the velocity increases 0.8 m/s. So, the acceleration is 0.8 m/s2.

(c) The sled starts from rest with an acceleration of 0.8 m/s2.

`v^2 = v_0^2 + 2ax\\v^2 = 0 + 2(0.8)(14.4)\\v = 4.8~{\rm m/s}`

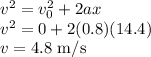
(d) The following kinematics equation will yield the time:

`\Delta x = v_0 t + (1)/(2)at^2\\14.4 = 0 + (1)/(2)(0.8)t^2\\t = 6~{\rm s}`

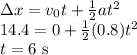
(e) The same kinematics equation will yield the displacement:

`\Delta x = v_0t + (1)/(2)at^2\\\Delta x = (4.8)(1) + (1)/(2)(0.8)1^2\\\Delta x = 5.2~{\rm m}`