Answer:
Hence The composition
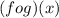 of the given function is
of the given function is
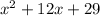 .
.
Explanation:
Given:
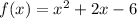

We need to find
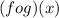 .
.
Solution:
Now we can say that;
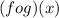 =
=
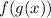

Now Applying distributive property we get;
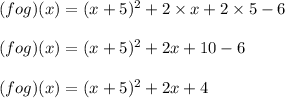
Now Solving the exponent function we get;

Hence The composition
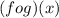 of the given function is
of the given function is
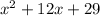 .
.