Question

Can a goalkeeper at her/ his goal kick a soccer ball into the opponent’s goal without the ball touching the ground? The distance will be about 95 m. A goalkeeper can give the ball a speed of 30 m/s.

Answer 1

No she cannot.

Step-by-step explanation:

Let
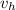`v_h` be the horizontal component of the ball velocity when it's kicked, assume no air resistance, this is a constant. Also let
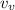`v_v` be the vertical component of the ball velocity, which is affected by gravity after it's kicked.

The time it takes to travel 95m accross the field is

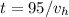`t = 95 / v_h` or
`v_h = 95/t`

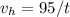
t is also the time it takes to travel up, and the fall down to the ground, which ultimately stops the motion. So the vertical displacement after time t is 0

`s = v_vt + gt^2/2= 0`

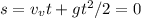
where g = -9.8m/s2 in the opposite direction with
`v_v`

`v_vt - 4.9t^2 = 0`

`v_vt = 4.9t^2`

`v_v = 4.9t`

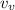
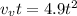
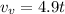
Since the total velocity that the goal keeper can give the ball is 30m/s

`v = v_v^2 + v_h^2 = 30^2 = 900`

`(4.9t)^2 + \left((95)/(t))^2 = 900`

`24.01t^2 + (9025)/(t^2) = 900`

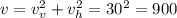
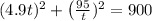
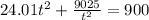
Let substitute x =
`t^2` > 0

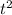`24.01 x + (9025)/(x) = 900`

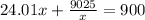
We can multiply both sides by x

`24.01 x^2 + 9025 = 900x`

`24.01x^2 - 900x + 9025 = 0`

`t= (-b \pm √(b^2 - 4ac))/(2a)`

`t= (900\pm √((-900)^2 - 4*(24.01)*(9025)))/(2*(24.01))`

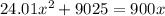
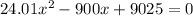
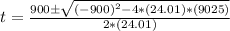
As
`(-900)^2 - 4*24.01*9025 = -56761 < 0`

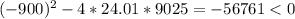
The solution for this quadratic equation is indefinite

So it's not possible for the goal keeper to do this.