Question

Assuming complete dissociation of the solute, how many grams of KNO3 must be added to 275 mLmL of water to produce a solution that freezes at −−14.5 ∘C? The freezing point for pure water is 0.0 ∘C∘C and Kf is equal to 1.86 ∘C/m.If the 3.90 m solution from Part A boils at 103.45 ∘C, what is the actual value of the van't Hoff factor, i? The boiling point of pure water is 100.00 ∘C and Kb is equal to 0.512 ∘C/m.

Answer 1

1) 108.27 grams of potassium nitarte must be added to 275 mL of water to produce a solution that freezes at -14.5°C.

2) 1.73 is the actual value of the van't Hoff factor, i.

Step-by-step explanation:

1) Formula used depression in freezing point ;

`\Delta T_f=T-T_f`

`\Delta T_f=i* K_f* m`

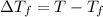
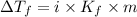
where,

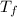`T_f` =Freezing point of solution

T = Freezing point of water

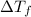`\Delta T_f` =depression in freezing point =

i = van't Hoff factor of solute

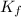`K_f` = freezing point constant

m = molality of solution

We have :

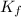`K_f` of water = 1.86°C/m ,

Molality of solution = m = ?

`KNO_3(aq)\rightarrow K^+(aq)+NO_3^(-)(aq)`

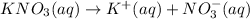
i = 2

Freezing point of solution =
`T_f=-14.5^oC`

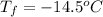
Freezing point of pure water = T = 0°C

`\Delta T_f=T-T_f`

`\Delta T_f=0^oC-(-14.5 ^oC)=14.5^oC`

`14.5^oC=2* 1.86^oC* m`

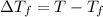
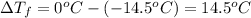
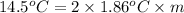
m = 3.898 molal

3.898 moles of potassium nitrate is dissolved in 1 kg of water or 1000 g of water.

Volume of water , V= 275 ml

Mass of water = m

Density of water= d = 1 g/mL

`m=d* V=1 g/ml* 275 mL = 275 g`

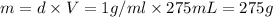
Here, 3.898 moles of potassium nitrate is dissolved in 1 kg of water or 1000 g of water. Then moles of potassium nitarte present in 275 grams of water is :

`(3.989 mol)/(1000)* 275 =1.072 mol`

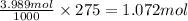
Mass of 1.072 moles of potassium nitrate :

1.072 mol × 101 g/mol = 108.27 g

108.27 grams of potassium nitarte must be added to 275 mL of water to produce a solution that freezes at -14.5°C.

2) Formula used an Elevation in boiling point;

`\Delta T_b=T_b-T`

`\Delta T_b=i* K_b* m`

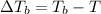
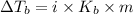
where,

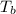`T_b` =boiling point of solution

T = boiling point of water

`\Delta T_b` =Elevation in boiling point =

i = van't Hoff factor of solute

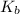`K_b` = Boiling point constant

m = molality of solution

of the solution

We have :

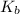`K_b` of water = 0.512°C/m ,

Molality of solution = m = 3.90 m

i =?

The boiling point of pure water = T = 100.00°C

The boiling point of solution =
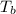`T_b`= 103.45°C

`\Delta T_b=103.45^oC-100.00^oC=3.45^oC`

`\Delta T_b=i* K_b* m`

`3.45^oC=i* 0.512 ^oC/m* 3.90 m`

`i=(3.45^oC)/(0.512 ^oC/m* 3.90 m)=1.73`

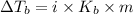
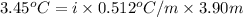
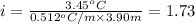
1.73 is the actual value of the van't Hoff factor, i.