Let
 and
and
 be the length and height, respectively, of the rectangle.
be the length and height, respectively, of the rectangle.
Let the bottom left vertex be the origin (0, 0), and position the triangle so that the bottom leg lies on the horizontal axis in the
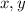 -plane. The hypotenuse of the triangle then lies on the line through (0, 0) and (6, 8), with slope 8/6 = 4/3. Then for some
-plane. The hypotenuse of the triangle then lies on the line through (0, 0) and (6, 8), with slope 8/6 = 4/3. Then for some
 between 0 and 6, we have
between 0 and 6, we have
 .
.
This means for some fixed distance
 from the origin, the rectangle has length
from the origin, the rectangle has length
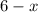 and height
and height
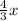 . Thus the area of the rectangle can be expressed completely in terms of
. Thus the area of the rectangle can be expressed completely in terms of
 as
as
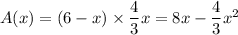
Non-calculus method:
Complete the square to get
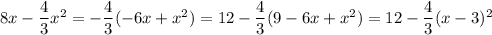
which is maximized when the quadratic term vanishes at
 , giving a maximum volume of
, giving a maximum volume of
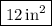 .
.
Calculus method:
Differentiate
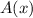 and find the critical points.
and find the critical points.

Differentiate again to check the sign of the second derivative at the critical point.
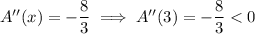
which indicates a local maximum at
 . Hence the maximum area is
. Hence the maximum area is
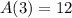 , as before.
, as before.