Answer:
B. Geometric sequence.
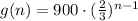
Explanation:
We have been given that Wanahton purified a portion of water with 900 grams of contaminants. Each hour, a third of the contaminants was filtered out.
The amount of contaminants remaining after each hour would be 2/3 of the previous hour amount as 1/3 of contaminants was filtered.
Since amount is not constant, therefore, the sequence would be geometric.
We know that explicit formula for geometric sequence is in form
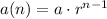 , where,
, where,
a = First term,
r = Common ratio.
For our given scenario
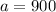 and
and
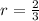 , so our required formula would be:
, so our required formula would be:
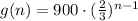
Therefore, an explicit formula for the given geometric sequence would be
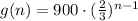 .
.