Question

Two 27.0-g copper spheres are placed 77.0 cm apart. Each copper atom has 29 electrons, and the molar mass of copper is 63.5463 g/mol. What fraction of the electrons from the first sphere must be transferred to the second sphere for the net electrostatic force between the spheres to equal 200 kN?

Answer 1

78000 electrons

Step-by-step explanation:

The force of attraction between the two charges is given as

F = Kq1q2/ r^2

Since the charges are equal

q1= q2

F = kq^2/r^2

Making q as the subject of the formulas

q = r × √F/k

q = 77× 10^-2 m × √ 200× 10^3 / 9 × 10^ 9 Nm^2/C^2

= 0.77 × √ 22.22× 10^-6

=0.77 × 4.714 × 10^ -3

q = 3.63 ×10^-3 C

= 3.63mC

The fraction of electron to be transferred from the first sphere to the second sphere

N = q/e ; relationship between number of electrons and charge

With copper atom having 29 electrons

= 3.63 × 10^-3/ 1.6 × 10^-9 ×29

3.63 × 10^-3 /46.4 × 10^ -9

N = 0.078 × 10 ^ 6

N =78000 electrons that will be transferred

Answer 2

The fraction of the electrons from the first sphere that must be transferred to the second sphere is 2.2687 X 10¹⁶ Electrons

Step-by-step explanation:

From coulomb's law;

`F = (K*q_1q_2)/(r^2)`

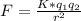
where;

F is the electrostatic force between the two spheres = 200 X 10³ N

k is coulomb's constant = 8.99 X 10⁹ Nm²/C²

q₁ is the charge on first sphere

q₂ is the charge on second sphere

r is the distance between the two spheres = 77cm = 0.77m

Since the two sphere have equal mas, the magnitude of their charge will be same = q

`F = (K*q^2)/(r^2)`

`q^2 = (F*r^2)/(K), then, q = \sqrt{(F*r^2)/(K)} = r\sqrt{(F)/(K)}`

`q = (0.77)\sqrt{(200000)/(8.99X10^9)} = 0.0036344 C`

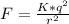
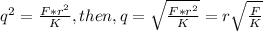
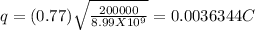
q = 3.6344 X 10⁻³C

The magnitude of charge on each sphere is 3.6344 X 10⁻³C

To find the number of electrons transferred

N = q/e

where;

N is the number of electrons transferred

q is the charge on each sphere

e is the charge on one electron = 1.602 X 10⁻¹⁹ C

N = (3.6344 X 10⁻³)/(1.602 X 10⁻¹⁹)

N = 2.2687 X 10¹⁶ Electrons

The fraction of the electrons from the first sphere that must be transferred to the second sphere is 2.2687 X 10¹⁶ Electrons