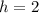Answer:
Explanation:
Alrighty let's do this.
We know that formula for the Area of a triangle is:
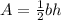
They give us the area as
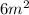 , so let's include it in the equation.
, so let's include it in the equation.
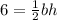
Now we reach a stage where we have 2 unknown variables! That means we can't solve it in its current state. So the idea you should have in cases like these where you have 2 or more unknown variables is, "Can I represent this one variable in terms of another variable?" In this case you can do exactly that. You can represent height in terms of length of the base. We are told the height of the triangle is 4 meters less than the base. That is telling us that
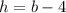
So replace
 in the equation with
in the equation with
 .
.
You will now get:
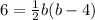
Now we can work towards solving. Let's get simplifying.
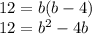
bring everything to one side so we can make a quadratic and factor:
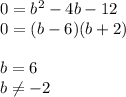
We get that
 .
.
Since we need the height of the triangle we'll need to call back on what h is. We found earlier that
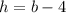 , so to find h, we just sub in our b value into that.
, so to find h, we just sub in our b value into that.
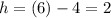
We find that