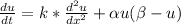Question

Derive an equation for the concentrationu(x,t) of a chemical pollutant, if the chemical is produced due to chemical reaction at the rate ofαu(β−u) per unit volume.

Answer 1

Explanation:

Given:

Rate k = αμ ( β - μ )

Find:

Derive an equation for the concentration u(x,t)

Solution:

- From the law of conservation we have:

`(d)/(dt)\int\limits^b_a {u (x,t)} \, dx = sig (a,t) - sig(b,t) + \int\limits^b_a {\alpha }u(\beta \ - u). dx`

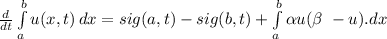
- After dividing the above expression by A i.e cross sectional area of the rod:

`0 = \int\limits^b_a ({(du)/(dt) + (dsig)/(dx) - \alpha u(\beta - u)).dx} \,`

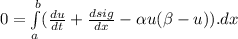
- This is valid for any for any interval [ a, b ] , and the integral is 0:

`0 = {(du)/(dt) + (dsig)/(dx) - \alpha u(\beta - u)`

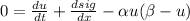
- Now use Fick's law we will obtain a PDE only as a function of u:

`(du)/(dt) = k*(d^2u)/(dx^2) + \alpha u (\beta - u)`